3-даражадагы көп мүчө деген эмне?

2025 Автор: Lynn Donovan | [email protected]. Акыркы өзгөртүү: 2025-01-22 17:31

Үчүнчү даражадагы көп мүчөлөр куб катары да белгилүү көп мүчөлөр . Кубиктердин мындай өзгөчөлүктөрү бар: Бирден үчкө чейин тамырлар. Эки же нөл экстрема. Тамырлар радикалдар тарабынан чечилет.

Анда 3-даражадагы көп мүчөнүн 4 кесилиши болушу мүмкүнбү?

Рэй дейт үчүнчү - даражадагы көп мүчөнүн 4 кесилиши бар . Ооба алар болот экөө тең туура, анткени алар болушу мүмкүн а үчүнчү даражадагы көп мүчө бул х огунан үч жолу жана у огун бир гана жолу кесип өтөт. Демек, эгер ошондой болсо, анда алар мүмкүн экөө тең туура болот.

Ошо сыяктуу эле, 4-даражадагы көп мүчө деген эмне? Төртүнчү даражадагы көп мүчөлөр квартик катары да белгилүү көп мүчөлөр . Квартиктер мындай мүнөздөмөлөргө ээ: Нөлдөн төрткө чейин тамырлар. Бир, эки же үч экстрема. Нөл, бир же эки ийилүүчү чекиттер.

Анын үстүнө, 3 деген даража деген эмне?

3x бар даража 1ден (x көрсөткүчү 1ге барабар) 5y ³ бар даражасы 3 (y көрсөткүчү бар 3 ) 3 бар даража 0 (өзгөрүүчү жок)

Факторду кантип табасыз?

" Факторлор " бул башка санды алуу үчүн көбөйткөн сандар. Мисалы, факторлор 15тин саны 3 жана 5, анткени 3×5 = 15. Кээ бир сандар бирден ашык факторизацияга ээ (бир нече факторлорго бөлүү жолу). Мисалы, 12 1 × 12, 2 × 6 же 3 × 4 катары факторлорго бөлүүгө болот.

Сунушталууда:

Javaдагы статикалык мүчө деген эмне?

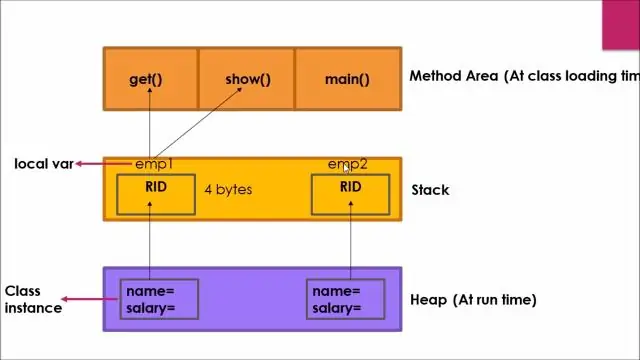
Java 8 Объектке багытталган программалоо программалоо. Java тилинде статикалык мүчөлөр класска тиешелүү жана сиз классты түзбөстөн бул мүчөлөргө кире аласыз. Статикалык ачкыч сөздү методдор, талаалар, класстар (ички/уяланган), блоктор менен колдонсо болот